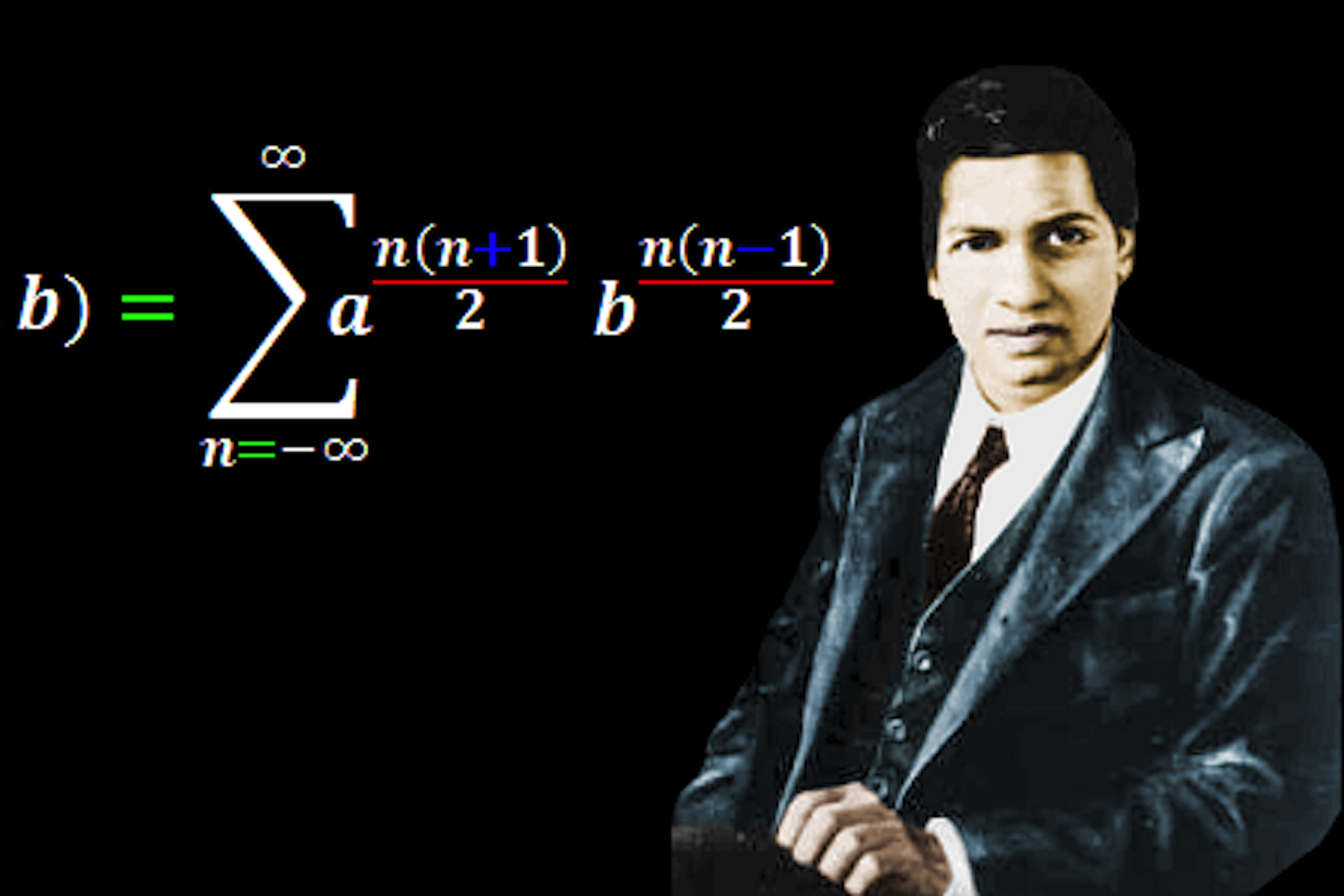Srinivasa Ramanujan’s story is one of the great romantic tales of mathematics. It is an account of triumph and tragedy, of a man of genius who prevailed against incredible adversity and whose life was cut short at the height of his powers. Ramanujan, a self-taught mathematician born in a rural village of South India, is said to have spent so much time thinking about mathematics that he failed college, twice. His wife and family would feed him by hand so that he didn’t have to stop doing his sums, according to his wife Janakiammal.
It is also a story about how Ramanujan, a deeply religious Hindu, credited his substantial mathematical capacities to divinity and stated that the mathematical knowledge he displayed was revealed to him by his family goddess. “An equation for me has no meaning,” he once said, “unless it expresses a thought of God.” He was seemingly blissfully unaware of the fact that during the last half of 19th century the results of science, mathematics and the beliefs of religion, had come into a position of frank disagreement, from which there can be no escape, except by abandoning either the clear teachings of science or the clear teachings of religion.
Whilst in the contemporary public sphere the most prominent interaction between science and religion concerns evolutionary theory, creationism and intelligent design. There is the real possibility that all our ideas will be looking at it from a wrong perspective if we think that this recurring perplexity was confined to contradictions between religion and science, and that in these controversies religion was always wrong and science always right. A century on, Ramanujan’s work hasn’t only remained extraordinarily forward-looking, his approach to mathematics and his search for mathematical elegance in early 20th century social customs, caste and divinity has fostered plentiful debate amongst philosophical scientists, theologians, and historians. The question is: are there social, religious or ethnic limitations on the validity of what a scientist discovers?
Ramanujan’s determination to lift himself from abject poverty, to be accepted and acknowledged as a first-class mathematician was not at the cost of the social customs and caste prejudices of early 1900s. And, it was not at the cost of bolstered self-regard, nor exalted confidence, which was something plainly evident in correspondence with the Cambridge University mathematician, G.H. Hardy. On, or about, 31 January 1913 the 36 year-old Hardy, already recognized as the leading English pure mathematician of his day, received Ramanujan’s first letter, below.
I beg to introduce myself to you as a clerk in the Accounts Department of the Port Trust Office at Madras on a salary of only £20 per annum. I am now about 23 years of age. I have had no University education, but I have undergone the ordinary school course. After leaving school I have been employing the spare time at my disposal to work at Mathematics. I have not trodden through the conventional regular course, which is followed in a University course, but I am striking out a new path for myself. I have made a special investigation of divergent series in general and the results I get are termed by the local mathematicians as ‘startling’.
I would request you to go through the enclosed papers. Being poor, if you are convinced that there is anything of value, I would like to have my theorems published. I have not given the actual investigations, nor the expressions that I get, but I have indicated the lines on which I proceed. Being inexperienced I would very highly value any advice you give me. Requesting to be excused for the trouble I give you.”
Yours very sincerely
Ramanujan
From the time Ramanujan travelled to Trinity College, Cambridge, to work with the mathematicians Hardy and Littlewood in March 1914 until ill health compelled his return to India where he died at the age of 32, he had achieved his lifelong ambition: to have his mathematical ideas validated by professional mathematicians.
During his short life, Ramanujan independently compiled nearly 4000 identities, many of which are completely novel, original, and highly unconventional. Eventually, though, the frustrated Ramanujan spiralled into depression and illness, even attempting suicide at one point. His last letters to Hardy, written in January 1920, show that he was still continuing to produce new work. His ‘lost notebook’, which was really a collection of loose and unordered worksheets written in his distinctive handwriting, were rediscovered by the American mathematician George Andrews in 1976. It took almost 50 years to discover these papers because they were in a box of effects of G. N. Watson stored at the Wren Library at Trinity College. They were earmarked to be thrown away. Andrews’ account of the discovery of the notebooks is in itself a story of perseverance, fortuitous timing, intrigue and much luck.
Madras 1913
Immediately before the war, Madras was a thriving urban metropolis; a central administrative centre for the British in India’s south. Flanked by a seaport township and linked by The Madras Railway Company to Mumbai in the west and the tea plantations of Bengaluru in the south. Madras was one of only three major cities having a telephone exchange and was well on its way to becoming one of south India’s largest cultural, economic and educational centres.
In 1913 Moses and Company, the tailors on Mount Road, were advertising their woollen suits and woollen underwear for Europe-bound students. Madras Corporation was debating the closure of a road in Santhome; others, many more likely, were preoccupied by the Golu or festive display of dolls in the late autumn year. Travelers, merchants, mostly British, mostly men of the empire would take tea at the old Spencer’s hotel. Under lethargic, unhurried fans, birds chirping in the shade of the Fish Tail palms, they would confer over affairs of the subcontinent. Outside, there would be women in their cool saris and ribboned children on their way to school. Schools, at least according to finicky British-India records, were benefiting from a British [Christian] missionary education.
This fact has some bearing on how some students integrated their faith, undoubtedly Hindu, with Christian teachings, as well as how this formed their outlook on science and mathematics. Years later, one such student would write: “I discovered a wonderful synthesis between my faith and the cutting edge of science. It helped me to understand that science and spirituality aren’t mutually exclusive. I also saw how much faith we place in the field of science and its theories.”
Madras, old but otherwise in good condition according to The Times of India compered an unlikely union. Madras may well have been in good condition but that was really a matter of perspective. Almost half a million people, many of them Hindu, nearly all unskilled, earned their living as street hawkers, street sellers, taxi drivers, mechanics and in other manual or industrial trades. Bare-bodied men would strain with heavily-laden carts – some pulling from the front, others pushing from behind up the steps of the bridges in front of the Central Station and near Stanley Hospital in the scorching mid-day heat. It was here that Ramanujan lived in extreme poverty and often on the brink of starvation. He would go door to door looking for work.
Some of the handcart pullers would tie a sack-cloth around their feet. In those days, the poor from neighbouring villages migrated to the city in search of work. They came with nothing from their homes. They bathed, ate and slept on the railway platforms, some on the pavements. There would be light of the most dazzling colours, of mirrored bangles that glistened from rickety market stalls gilded with flags that blew calmly in the warm Indian breeze. Fragrant sacks would be stacked high in winding narrow alleyways, spice lanes that slapped the air with aromatic flavours that were never less than evocative and visceral.
Ramanujan was poor, but here were a people maintained a deeply rooted conviction in the interconnectedness of life and the sanctity of nature. A faith tempered in ceremony, prayer and sacrifice. Their temples were blessed and among the holiest places; for the people it was a way of looking at devotion almost metonymically, a love for the city shouldered on the shape of idols, temples, and shrines. These had, after all, received a visit by the Saivite saints Nayanars.
In December and January there was a festival for women. Unmarried women would observe a partial fast on this day to ‘get good husbands’ and married women would take a fast from the preceding day and on the day of Thiruvathira for the well-being of their husband and family. In this year, a young 10-year-old Janakiammal from Rajendram, a village close to Marudur Railway Station was such a patnee hona, or a wife-to-be.
The Ramanujan-Janakiammal wedding was a five-day ceremony and it took place along with the wedding of another sister of Janakiammal. They resided at Saiva Muthaiah Mudali Street, in George Town. In this year the 21-year-old Ramanujan joined the University of Madras as its first research scholar. His wife and mother lived with him before Ramanujan left for England, on 17 March, 1914. Janakiammal joined him on his return to Madras and nursed him till his untimely death on 26 April, 1920.
European influences were strongest in the towns of India. This was especially true in the old bases of British trade, such as Calcutta, Madras or Bombay, where a new Indian intelligentsia had begun to take root. Whatever the British may have intended, their early rule seems generally to have consolidated the hold of what they regarded as ‘traditional’ intellectuals, rather than displacing them with new ones and the authority of Brahmins and of doctrines of caste separation grew stronger.
In the early 1900s Madras was a place, a home, to a population exhibiting ominous signs. They would soon sweep away coalescence and shape a drama that would unfold in the coming short years and make Mohandas Karamchand Gandhi a household name both in India and across the world. It was a nation less inclined to meddlesome formality and officious bureaucracy – less inclined to submit to a colonial resolve of a different king, a different time and a different god.
India was also a nation at once assured of its unfailing patriotism and peasant-born nationalism. Never quite the classic modern nation state, it was instead a civilisation swathed in deep tradition, religion, people and creatures that held a place of their own in the Hindu pantheon as vehicles of gods and goddesses. This was also a time when a movement, a groundswell that had taken hold in the 1850s, continued to inspire the anti-colonial and reformist trends, emerging during the freedom struggle and squarely criticizing the caste system, feudal exploitation, patriarchy and superstition.
The call to Trinity College
The young Ramanujan didn’t at first jump at the opportunity to work and study with some of the best mathematicians at the turn of the 20th century. It’s entirely possible that his naïve, meek and unimposing assessment of himself prevented him from entirely appreciating the immeasurable opportunity – the gift really – that Hardy and Littlewood had offered him.
It was an invitation to an ill-educated, jobless unknown to one of England’s finest universities. Among Trinity’s mathematicians have been John Dee, author of an important Mathematical Preface to the first English translation of Euclid’s Elements of Geometry, Isaac Newton who formulated a version of calculus and the principles of universal gravitation and of course Stephen Hawking, who was a graduate student at Trinity Hall. Later, he would hold the title as Lucasian Chair of Mathematics as had Isaac Newton, Paul Dirac, Joseph Larmor, Charles Babbage, George Stokes. Likewise, Hardy and Ramanujan will be remembered as titans of the College.
Ramanujan would have been anxious to travel. As a strict Brahmin, crossing the seas to foreign lands causes the loss of one’s social respectability, as well as the putrefaction of one’s cultural character and posterity. It wasn’t until early 1914 that Ramanujan gained his mother’s consent to make his passage to England. There were to be more obstacles. He was deeply conflicted by his desire to pursue his mathematics and at the same time conform to the social and religious customs of the day. According to his wife Janakiammal, Ramanujan had sought the blessing of the family’s favourite deity, the Goddess Namagiri. And as such, or as a kind of concession he sought Hardy’s assurance, modestly, that his diet of fruits, vegetables, beans and grains could be adhered to in England.
Hardy was aware that E.H. Neville, another fellow of Trinity College was planning to make a trip to Madras at this time and tasked him with helping Ramanujan. A relieved Ramanujan writes to Hardy in January 1913: “Dear Sir, I learnt from Mister Neville that you are anxious to get me to Cambridge.” He goes on: “I went to the colleague of your College who very kindly spoke to me and cleared my doubts. I need not care for my expenses, that my English is adequate, that I need not to appear for any examination and that I can maintain my vegetarian diet.”
Hardy had in fact asked Neville to help Ramanujan secure a scholarship from the University of Madras. Neville writes to the university that: “the discovery of the genius of S. Ramanujan of Madras promises to be the most interesting event of our time in the mathematical world …” Three years later, in April 1919, Ramanujan returns to India, emaciated from prolonged confinement in a sanatorium but now possessing a reputation. Questions regarding his diet and England’s inclement climate are seen by some as contributing to his ill-health and death in 1920 at the age of 32.
Hardy didn’t just discover Ramanujan, his care in mentoring him must be admired. This is particularly the case when we consider that Hardy was only a few years Ramanujan’s senior. Hardy’s main worry was how to teach this “astounding talent mathematics without destroying his confidence.”
The last thing Hardy wanted was to dent Ramanujan’s fearless approach to the most difficult of problems. He would write: “The limitations of his knowledge were as startling as its profundity. Here was a man who could work out modular equations, and theorems of complex multiplication, to orders unheard of, whose mastery of continued fractions was, on the formal side at any rate, beyond that of any mathematician in the world … It was impossible to ask such a man to submit to systematic instruction, to try to learn mathematics from the beginning once more.”
The last thing Hardy wanted was to dent Ramanujan’s fearless approach to the most difficult of problems.
Hardy lived on for some 27 years after Ramanujan’s death, to the old age of 70. When asked in an interview what his greatest contribution to mathematics was, Hardy unhesitatingly replied that it was the discovery of Ramanujan, and even called their collaboration: “… the one romantic incident in my life … and his death is one of the worst blows I have ever felt. But now I say to myself when I’m depressed and I find myself forced to listen to tiresome and pompous people, well, I have done something you have never done. I have collaborated with both Littlewood and Ramanujan on something like equal terms.”
However, Hardy, too, became depressed later in life and attempted suicide by an overdose at one point. Some have blamed the Riemann Hypothesis for Ramanujan’s and Hardy’s instabilities, giving it something of the reputation of a curse.
Genius
Shortly before he died, Hardy’s long-time collaborator Littlewood, mentioned two names: H. F. Baker and E. W. Hobson. They are both assumed to be the first recipients of Ramanujan’s letters. Neither was a particularly good choice: Baker worked on algebraic geometry and Hobson on mathematical analysis, subjects fairly far removed from what Ramanujan was doing. In any event, neither of responded. One can, while perhaps not sympathising with them, understand how they might have received his letters and their reaction.
For one thing, Ramanujan very rarely demonstrated derivation. As mentioned above, for him an equation meant nothing unless it expressed a thought of God. It’s highly probable, however, that he quite simply didn’t see the need, perhaps he didn’t know better, or he just didn’t know how. We know that his lack of formal training contributed greatly to his inability to communicate his ideas. We also know he was influenced by G.S. Carr’s coaching notes, a library copy he obtained from a friend when he was 16.
Carr’s text, A Synopsis of Elementary Results in Pure and Applied Mathematics, was in part written to teach bright English boys for university entrance exams and not necessarily the best example of demonstrating formal mathematical formulation. This text, made famous by Ramanujan, marked the real starting point of his career. Carr has sections on the obvious subjects: algebra, trigonometry, calculus and analytical geometry, but some sections are developed disproportionally, particularly the formal side of the integral calculus. The text aside, Ramanujan had exceptional mathematical intuition. He was highly instinctive with an ability to recognize patterns, differentiate and abstract.
The letter Baker and Hobson received included 120 pages of hand-written theorems, and described (as we now know) the special case of Riemann’s 1859 zeta function ζ(−1) for negative one. The Riemann hypothesis is a mathematical holy grail. Even today, the Clay Mathematics Institute regards the Riemann hypothesis as one of seven Millennium Problems attracting a prize of one million dollars for a correct solution. Ramanujan, for the record, hadn’t shown the Riemann hypothesis, but rather a special case. If Baker and Hobson didn’t recognize it, Hardy and Littlewood certainly did.
In 1910, Ramanujan met deputy collector V. Ramaswamy Aiyer, who founded the Indian Mathematical Society. Wishing for a job at the revenue department where Aiyer worked, Ramanujan showed him his mathematics notebooks. As Aiyer later recalled: “I was struck by the extraordinary mathematical results contained in the notebooks. I had no mind to smother his genius by an appointment in the lowest rungs of the revenue department.”
In the spring of 1913, Narayana Iyer, together with Ramachandra Rao and E. W. Middlemast, all of whom holding various positions in the Indian Mathematical Society, tried to present Ramanujan’s work to the British mathematician M.J.M. Hill of University College London. He commented that Ramanujan’s papers were riddled with holes. He added that although Ramanujan had “a taste for mathematics, and some ability”, he lacked the necessary educational background and foundation to be accepted by mathematicians. Yet, although Hill did not offer to take Ramanujan on as a student, he did give thorough and serious professional advice on his work.
With this, and with the help of friends, Ramanujan drafted the letters to Hardy. Ramanujan’s early letters included integrals Hardy himself was working on. In fact Hardy was so sufficiently proud of them he had them published. Seeing the same integrals in Ramanujan’s work, Hardy immediately realised that here was a mathematician of “[exquisite] taste.” In addition, there were formulas here that absolutely stunned him. Hardy says of these: “I have never seen anything least like them before – a single look at them is enough to show that they can only be written by a mathematician of the highest class. They must be true because if they were not true no one would have the imagination to invent them. The writer must be completely honest because great mathematicians are commoner than thieves or humbugs of such incredible skill.”
At Trinity College, Hardy and Littlewood thought that having Ramanujan travel to the College would allow them to better make sense of his results and the fragments of proofs he had provided through correspondence. It wasn’t at all clear to them how he was arriving at his results. It did seem he was experimenting with numbers, presumably to check if the results gave him an idea of what might be true. It’s not clear how he figured out what was actually true — and indeed some of the results he quoted weren’t in the end correct. But presumably he used some mixture of traditional mathematical proof, calculational evidence, and a lot of intuition. But he didn’t explain any of this to Hardy or Littlewood.
… presumably he used some mixture of traditional mathematical proof, calculational evidence, and a lot of intuition.
Just as it cannot be taken for granted that mathematics as a field of study is reflective of itself as a cognitive activity, it cannot be taken for granted that the ways in which one describes, understands, or even misunderstands an idea with which they have considerable formal experience is indicative of the processes by which that idea was first acquired. In this case Ramanujan is essentially self-taught, unpractised and predisposed to the most difficult of circumstances.
Shortly prior to Ramanujan setting sail to London, Littlewood writes to Harding, in an almost exact parallel of what Einstein says of Paul Dirac: “This balancing on the dizzying path between genius and madness is awful.” He added: “How maddening are his letters… in the circumstances I rather suspect that he’s afraid you will steal his work.” Afterwards, he wrote: “I received a letter from the War Office this morning, seems they need some assistance with ballistics.” Later, he writes to the atheist Hardy: “Please forgive this personal transcreation. I’m gone now to this god-awful war. I haven’t the faintest idea if I’ll ever return.”
On receipt of his letter
After dinner at Trinity one evening, some of the fellows adjourned to the combination room. Over their claret and port, Hardy mentioned to Littlewood some of the claims he had received in the mail from this unknown Indian. Some assertions they knew well; others they could prove; others they could disprove. But many they found not only fascinating and unusual but impossible to resolve. This to-ing and fro-ing between Hardy and Littlewood continued for the next day and beyond, and soon they were convinced that their correspondent was a genius. Accordingly, Hardy sends an encouraging reply to Ramanujan, which led to a frequent exchange of letters.
It was clear to Hardy that Ramanujan was totally exceptional. However, in spite of his amazing feats in mathematics, he lacked the basic tools of the trade of a professional mathematician. Hardy knew that if Ramanujan was to fulfil his potential, he had to have a solid foundation in mathematics, at least as much as the best Cambridge graduates.
His work on the Partition function with Hardy was the precursor of what is now called the circle method in analytic number theory and has played a crucial role in discoveries in number theory. The work on probabilistic number theory which has also played a significant activity in the 20th century has its origin in a paper Ramanujan and Hardy developed. Littlewood once remarked that: “every positive integer was one of Ramanujan’s personal friends.”
To that end, shortly before Ramanujan’s passing, Hardy remembers going to see him when he was ill at Putney: “I had ridden in taxi cab number 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavourable omen. ‘No,’ he replied, ‘it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways.’ The two different ways are: 1729 = 13 + 123 = 93 + 103.”
His Hinduism
Various aspects of the relationship between religion and science have been addressed by modern historians of science and religion, and others from various geographical regions and cultures. After thinking about Ramanujan, Andrews concluded that there are no social, religious or ethnic limitations on the validity of what a scientist discovers. The discovery of scientists of one civilisation or nationality can be received, assessed and assimilated by scientists of any other civilisation or nationality – assuming, of course, that the receptive scientist is sufficiently informed regarding the state of a subject and has the intelligence and scientific training to comprehend what is offered to him.
The mathematics that Ramanujan did in India was assessed by highly accomplished British mathematicians. So much so, that they could retrace the steps that his initiative powers had enabled him to leap over. It was not the Indian-ness of the Ramanujan mathematics that baffled the first British mathematicians, Hopson and Baker; rather it was his exceptionally advanced originality. It required two mathematicians of very high quality, Hardy and Littlewood to appreciate it, to learn from it and to contribute to Ramanujan’s work.
As the years passed, the notebooks have been studied, interpreted, proven and assimilated by Western mathematicians. I have not read any references to the specifically Indian character of Ramanujan’s mathematics. His maths is maths, indifferent to the place and circumstance of its creation.
An intimate, reciprocal relationship between genius and tradition is evident in the case of Ramanujan. He made a connection with some older and incomplete condensations of the traditions of mathematics developed in Europe. He retraced, in his own way and in ignorance of them, paths of the tradition that had already been traversed in Europe. In other respects, he shot well ahead of the points reached by the movement and tradition of Europe. It is unlikely that the tradition of the Hindu belief in which Ramanujan participated steadfastly obstructed his advances from the traditions of mathematics that had developed in Europe. Ramanujan thought that the Hindu Gods in whom he believed had in fact inspired his mathematical advances.
This article was published in the June 2021 edition (vol. 121) of Australian Rationalist.